Jim Cronin - Development Time and Predator-Prey Population Dynamics

Development Time and Predator-Prey Population Dynamics

Project Overview

C. maculatus and A. calandrae — Fig. 1. The (A) host *C. maculatus* and (B) parasitoid *A. calandrae*

Understanding the mechanisms promoting stability of predator-prey/parasitoid-host interactions has been a fertile and critically important area of theoretical and empirical research for the past century. Age (stage) structure, differential vulnerability of prey life stages, and variability in development times of life stages are ubiquitous features of predator-prey systems. Theoretical studies have demonstrated that stability is enhanced by invulnerable host stages, that the interaction between parasitoid and host can induce generation cycles in the host, and recently that variability in host (or parasitoid) development can strongly enhance stability. To date, there has NEVER been an unambiguous test of these theoretical predictions. Using the cowpea weevil Callosobruchus maculatus and its parasitoid Anisopteromalus calandrae as a model predator-prey system (Fig. 1), we are tested whether a change in the mean and/or variability in development time of specific host stages can affect host-parasitoid stability and dynamical behavior.

Fig. 2. John Reeve observing planthopper boundary behavior.

This project involved my long-time collaborator, John Reeve (Fig. 2), and two mathematicians at Southern Illinois University, Dashun Xu and MingQing Xiao. The research was funded by a grant from NSF (Population and Community Ecology/Mathematical Biology).

Research Objectives

This research project had five objectives.

(1) Conduct the first experimental tests of whether variability in development time of the vulnerable host stage can affect host-parasitoid stability and long term population dynamics.

(2) Test the long-standing theoretical prediction that the mean duration of an invulnerable host stage affects host-parasitoid stability and long term population dynamics.

(3) Experimentally test how changes in the pulse addition of food resources affects host-parasitoid stability and long-term population dynamics.

(4) Evaluate how changes in the duration and variability in development time of prey life stages influences the evolution of predator morphological and life-history traits.

(5) Develop more realistic mathematics models to describe complex parasitoid-host interactions.

Fig. 3. Experimental microcosm containing mung beans, weevils and parasitoids

Variance in vulnerable host stage experiment:

Cronin, J. T., J. D. Reeve, D. Xu, M. Xiao and H. N. Stevens. 2016. Variable prey development time suppresses predator-prey cycles and enhances stability. Ecology Letters 19:318-327.

For two years (≈ 27 host generations), replicate host-parasitoid microcosms (Fig. 3) were subjected to two treatments, natural levels of variation (Normal variance) and high levels of variation (High variance) in the duration of the vulnerable host stage. We opted for an artificial means of changing development time that targets a specific life stage, the vulnerable stage of the host (H2 stage; Fig. 4), without altering any other aspects of the host’s demography. This was accomplished by manually replacing beans with weevils just prior to entering the vulnerable stage with weevils that have been in the vulnerable host stage for different lengths of time. Specifically, variability in the duration of the vulnerable host stage was increased by replacing weevils entering the vulnerable stage with equal numbers of weevils at the beginning and near the end of the vulnerable stage.

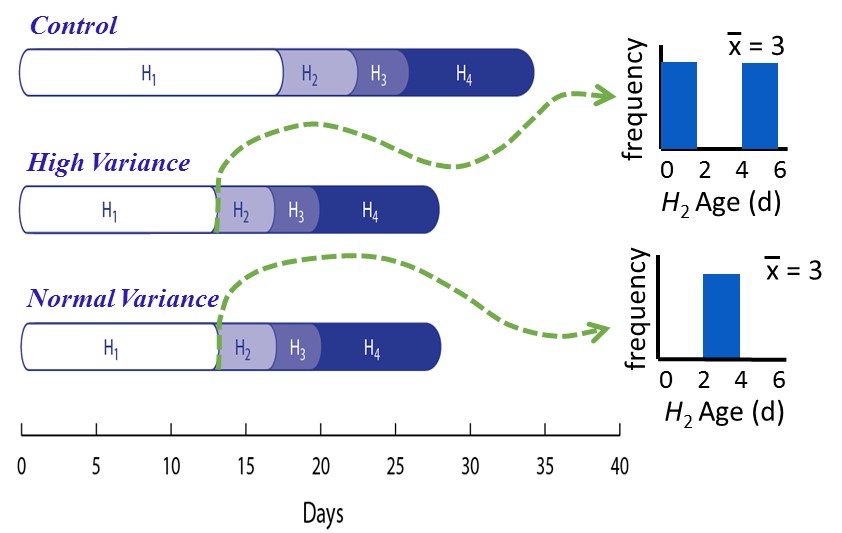
diagram of treatment effects — Fig. 4. Diagram of the experimental treatment and its effect on the average development times of the weevil life stages. For the adult weevil life stage (H4), the mean duration is based on the females. Inset histograms show the distribution of H2 weevil ages used in the High- and Low-variance treatments (Cronin et al. 2016).

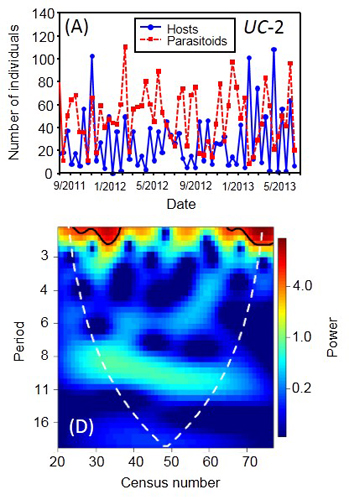
In unmanipulated control and Normal-variance microcosms, hosts and parasitoids exhibited distinct population cycles with a periodicity of 1 or 2 host generations, respectively (Figs. 5, 6). In contrast, microcosms in the High-variance treatment exhibited much more stable population dynamics (Fig. 6), in strong support of theoretical predictions above (Fig. 3). Adult host and parasitoid abundances were 18 and 24% less variable, respectively, in the High-variance than Normal-variance microcosms. More significantly, periodicity in host and parasitoid population dynamics all but disappeared. This study suggests that developmental variability is not simply noise in the system but is critical to predator-prey population dynamics. We suggest that variability in development times could be exploited in the development of pest-management programs. A manuscript from this research is currently in review for publication.

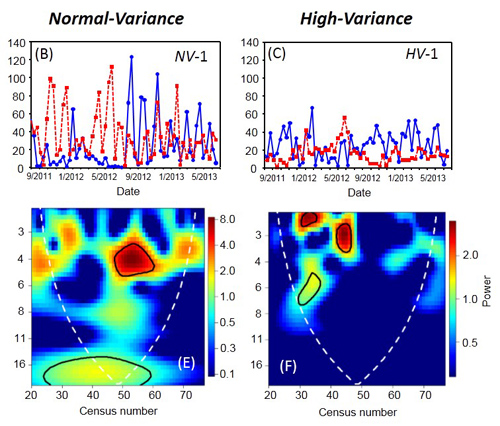
time series and wavelet analysis — Fig. 5. Time series and wavelet analysis for the host and parasitoid in a representative unmanipulated experimental microcosm. Spanning the two-year study, there is clear evidence of period-two oscillations (note the region in red in the wavelet analysis.)

Simulations using our stage-structured models for the host and parasitoid provided additional support that increasing variability in the duration of the vulnerable host stage, H₂, promotes increased system stability; i.e., reduced amplitude fluctuations and long-term persistence of the host-parasitoid interaction. We first estimated the parameters in the models using the data from the Unmanipulated controls, and found that the model readily generated period 2 oscillations similar to the microcosms (Fig. 7A) and found that the Normal-variance microcosms were prone to extinction whereas the High-variance microcosms were persistent, illustrating the stabilizing effect of variability. Fig. 7B-C shows the model output for these two treatments where stability was increased by adding more parasitoid aggregation, sufficient for the Normal-variance treatment to persist. The standard deviation in host population sizes was 60% higher for the Normal-variance as compared to the High-variance treatments. Standard deviation in parasitoid abundances between treatments was similar.

The simulations suggest that variability in the vulnerable host stage enhances stability because it allows some hosts to escape parasitism when parasitoid densities are high, allowing additional host cohorts to arise and thereby smoothing the oscillations.

model simulations — Fig. 7. Model simulations were tailored for each of the three treatments: Unmanipulated control (A), Normal variance (B) and High variance (C). In the Normal- and High-variance simulations, k (the clumping parameter from the negative-binomial model) was reduced to achieve long-term persistence in the Normal-variance treatment.

Duration of invulnerable host stage experiment:

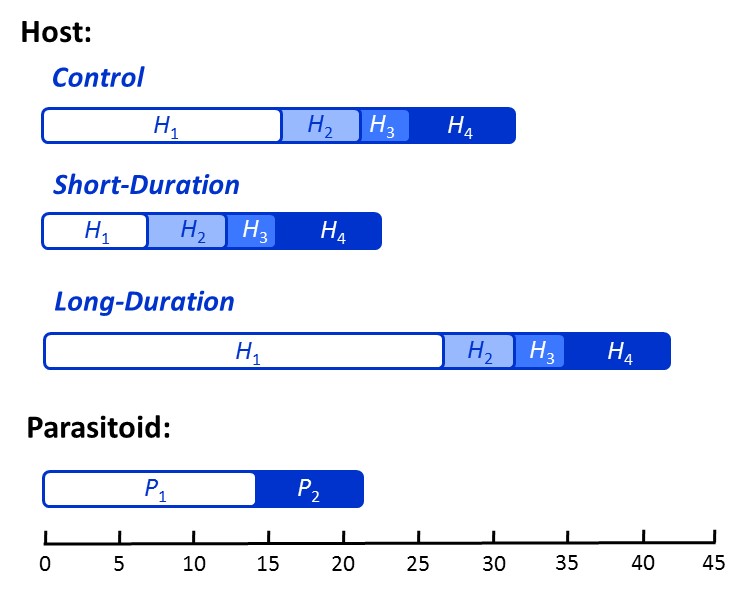
LDSD diagram — Fig. 8. Diagram of the experimental treatment of H₁ development time and its effect on the average development times of the weevil life stages. For the adult weevil life stage (H₄), the mean duration is based on the females.

The duration of certain life stages and relative lengths of the predator and prey life cycles can in theory have a strong influence on population dynamics. However, rigorous experimental tests of this theory are nonexistent. We conducted a microcosm experiment with the cowpea weevil (Callosobruchus maculatus) and its parasitoid (Anisopteromalus calandrae) to assess how a 60% increase (long-duration treatment) or 60% decrease (short-duration treatment) in the invulnerable prey stage affected host-parasitoid population dynamics (Fig. 8). We tested the prediction that stability is most likely for microcosms in the short-duration treatment, while generation cycles should occur for the long-duration and control treatments, with a longer period in the long-duration treatment.

The experiment was conducted between 2010 and 2013. Owing to an assortment of issues, modeling the long-term dynamics of this system in response to the experimental treatments took another decade to complete. However, a manuscript on this work has been submitted for review for publication (Cronin and Reeve in review).

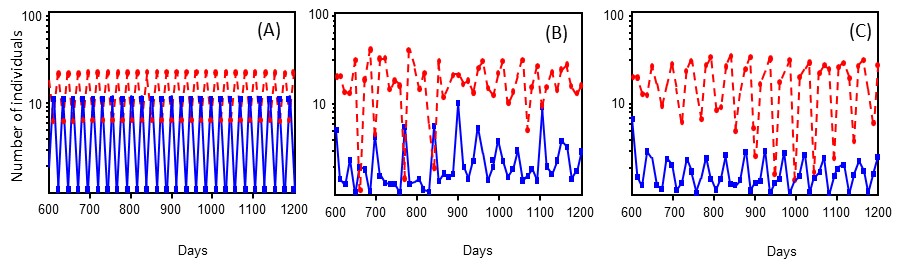
We found good support for most of the theoretical predictions. In the control treatment, persistent oscillations occurred with a period of about one generation as predicted by theory, while the long-duration treatment showed cycles similar to the control, rather than longer period ones. Representative time series for each treatment are reported in Fig. 9.

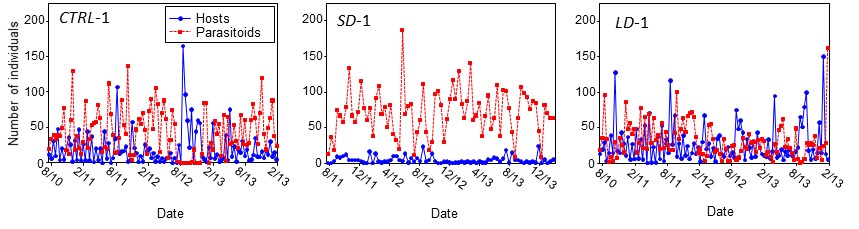
LDSD time series — Fig. 9. Representative time series for each treatment, the unmanipulated control (CTRL-1), Short-duration treatment (SD-1) and Long-duration treatment (LD-1).

Based on wavelet analyses for each time series, we found that in the short-duration treatment the cycles disappeared (Fig. 10), with the mean and SD in host densities reduced by 41-49% and 9-18%, respectively, relative to the other treatments.

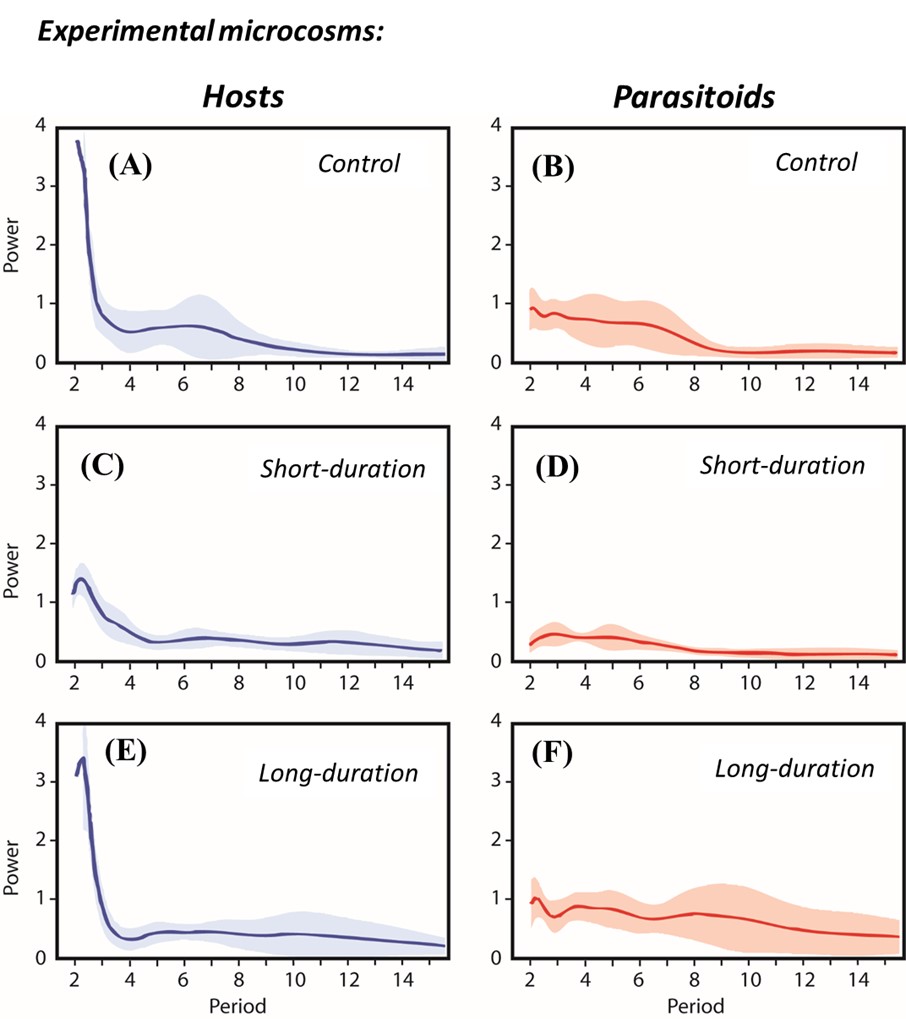
Fig. 10. Mean global wavelet spectrums for replicate experimental microcosms from the unmanipulated control (Host, A; Parasitoid, B), short-duration (C; D), and long-duration (E; F) treatments. For each treatment, the global wavelet spectrums were averaged among replicates. Bands represent 95% confidence intervals.

We also developed simulation models that closely matched the biological details and protocols used in the experiment, as well as simpler versions to understand how different features affected the dynamics. The short-duration and control models provided a close fit to the dynamics of these two treatments in the experiments. We were also able to duplicate the period of the oscillations in the long-duration treatment provided there was strong, contest-type competition in the weevil attack process. Finally, the simulations suggested that resource pulses can have a synergistic effect on inherent host-parasitoid cycles. We conclude that age structure and development time should be an important consideration in selecting agents for biological control and when evaluating causes of program success/failure.