Density-Dependent Emigration and Predator-Prey Population Dynamics
Project Overview
Dispersal can have major consequences for individual fitness, population dynamics, and species’ distributions. In light of the important need to predict how populations will respond to invasion and spread of alien species, habitat fragmentation, and climate change, understanding the causes and consequences of dispersal at both the patch and landscape levels is vital for population management and conservation.
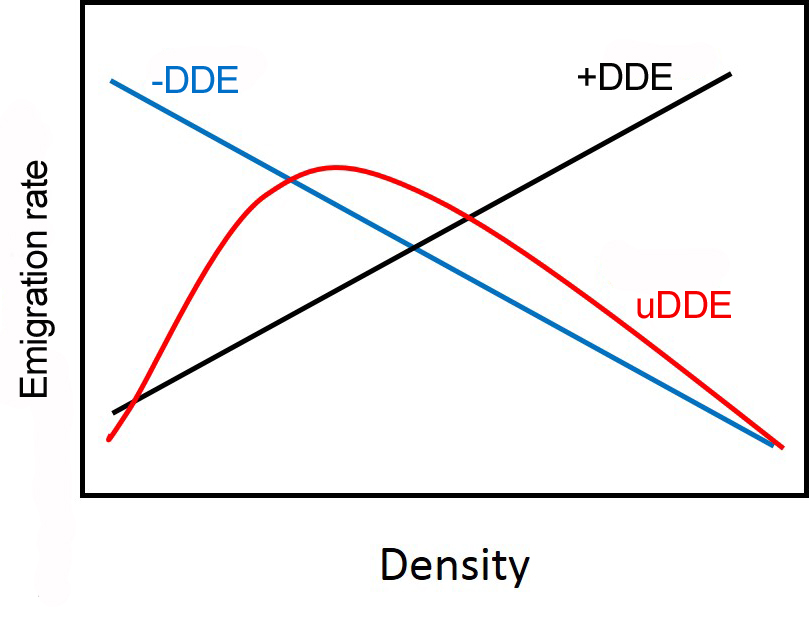
As the impact of dispersal on population dynamics is becoming increasingly recognized, the consequences and causes of dispersal have become a focus of much current research. Theoretical studies play an extremely important role in predicting the population level effects of dispersal. However, the assumptions of most theoretical models regarding the dispersal process often lack a great deal of realism. The paradigmatic view in ecology is that emigration is density independent (DIE) or positive density dependent (+DDE).
However, alternative forms are biologically plausible, including negative (-DDE), u-shaped (uDDE), and hump-shaped (hDDE) forms (Fig 1). Based on a review of the published literature (Harman et al. 2020) we found that the majority of studies exhibited DIE (30%) and +DDE (35%). However other forms were evident in the literature: –DDE (25%), uDDE (6%) and hDDE (4%). There was no taxon bias in the detection of different forms of DDE. We also developed a reaction-diffusion model to illustrate how different forms of DDE can affect patch-level population persistence. Based on our models, DIE and +DDE promoted stable and persistent populations. –DDE and uDDE generated an Allee effect that decreases minimum patch size. Lastly, -DDE and hDDE models yielded bi-stability that allows establishment of populations at lower densities. We conclude that the emigration process can be a diverse function of density in nature and that alternative DDE forms can have important consequences for population dynamics.
With joint funding from the NSF’s Mathematical Biology and Population and Community Ecology Programs (first grant in 2015, with renewals in 2019, 2022 and 2023), we have been examining how different forms of DDE, habitat fragmentation, competition (intra- and interspecific) and natural enemies can affect the population dynamics of natural and model systems. Experimental studies are being led by my Ph.D. student, Aaron Krivchenia, and me, using two species of Tribolium flour beetles and a fungal pathogen, Beauveria bassiana, as a model system. Mathematical models are being developed by Jerome Goddard (Dept. of Mathematics & Computer Science, Auburn University, Montgomery) and Ratnasingham Shivaji (Department of Mathematics & Statistics, The University of North Carolina at Greensboro) (see photo).

KEY FINDINGS:
Conspecific and interspecific competitor effect on movement and population dynamics
1. We developed a framework to facilitate the connection between small-scale movement and patch-level predictions of persistence through a mechanistic model based on reaction-diffusion equations (Cronin et al. 2019 Bulletin of Mathematical Biology). The model is flexible and can incorporate information about patch preference, movement behavior, and matrix-induced mortality. We mathematically analyzed the model’s predictions of persistence based on assumptions on the patch/matrix interface. Finally, we illustrated the utility of this framework with a well-studied planthopper species (Prokelisia crocea) living in a highly fragmented landscape. Qualitatively, the model results are in accord with experimental predictions regarding minimum patch size of P. crocea.
2. We extended the above reaction-diffusion model to account for the conditional dependency of dispersal (e.g., responses to patch boundaries, matrix hostility, competitors, and predators). In Acharya et al. (2023), we explored the dynamics of the diffusive Lotka–Volterra (L–V) competition model in such a fragmented landscape. In the case where competition is weak towards one species and strong towards the other, we find existence of a maximum patch size, and thus an intermediate range of patch sizes where coexistence is possible, in a patch surrounded by an intermediate hostile matrix when the weaker competitor has a dispersal advantage. These results support what ecologists have long theorized, i.e., a key mechanism promoting coexistence among competing species is a tradeoff between dispersal and competitive ability.
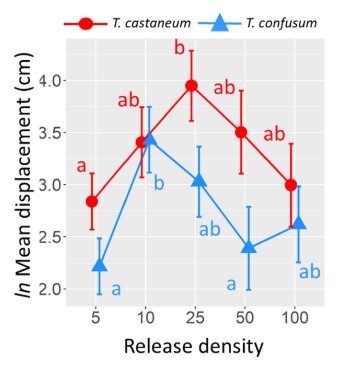
3. We demonstrated experimentally that Tribolium species within-patch movement depends on both intra- and interspecific density (Cronin et al. 2023). For both T. confusum (confused flour beetle; CFB) and T. castaneum (red flour beetle; RFB), within-patch movement was well described by a simple diffusion model. Moreover, mean displacement of both beetle species was hump-shaped with respect to conspecific density (Fig. 2). Finally, we found that both species of beetle impacted the within-patch movement rates of the other species. In both cases, it was total beetle abundance, not species identity that mattered to mean displacement. From this experimental work, we suggest that displacement or diffusion rates that exhibit a nonlinear relationship with density or depend on the presence or abundance of interacting species should be considered when attempting to predict the spatial spread of populations or scaling up to heterogeneous landscapes.
4. We used a theoretical spatially explicit population model built upon the reaction–diffusion framework to model a habitat specialist dwelling in islands of habitat surrounded by a hostile matrix to understand the mechanisms causing variation in density-area relationships, DAR(Goddard et al. 2022). Many studies spanning a wide diversity of taxa have described the DAR as positive, neutral, negative or some combination of the three. However, the mechanisms responsible for these relationships remain elusive. Our modeling results show that a single species following logistic-type population growth exhibits a strictly positive and continuous DAR. In the case of two species governed by diffusive Lotka–Volterra growth and competitive interactions, we observe that overall DAR structure can be either (1) positive, (2) positive for small areas and neutral for large, or (3) hump-shaped, i.e., positive for area below a threshold and negative for area above. We compared our theoretical results with two empirical studies (Anolis lizards on islands and crossbills and pine squirrels in forest fragments) where the pragmatic view of DAR fails to give a mechanistic understanding of what was observed. Close qualitative agreement between theoretical and observed DAR indicates that our model gives a reasonable explanation of the mechanisms underpinning DAR found in those studies. From a conservation perspective, the DAR is crucial to the identification of valuable habitat fragments that favor high abundance and the design of a reserve for a target species.
5. We demonstrated experimentally that Tribolium species emigration depends on both intra- and interspecific density (Krivchenia et al. in preparation A). As part of his dissertation research, Aaron Krivchenia conducted a 10-generation study to explore the effects of species composition (single species or two species), patch size and patch permeability on the population dynamics of T. confusum and T. castaneum. The experimental landscape consisted of a single patch with a surrounding hostile matrix (Fig. 3). Aaron manipulated patch size by adjusting the amount of flour in the central patch and manipulated patch permeability by varying the number of holes on either side of the central plastic box.

A decrease in patch size and increase in permeability typically lead to an increase in emigration of both Tribolium species, likely owing to increased competition and encounters with the boundary. When released alone, the two species exhibited +DDE (Fig. 4). In competition, RFB was DIE in relation to both species whereas CFB was -DDE to RFB, but the intraspecific effects varied from hDDE to uDDE across the RFB density gradient due to an interaction term.
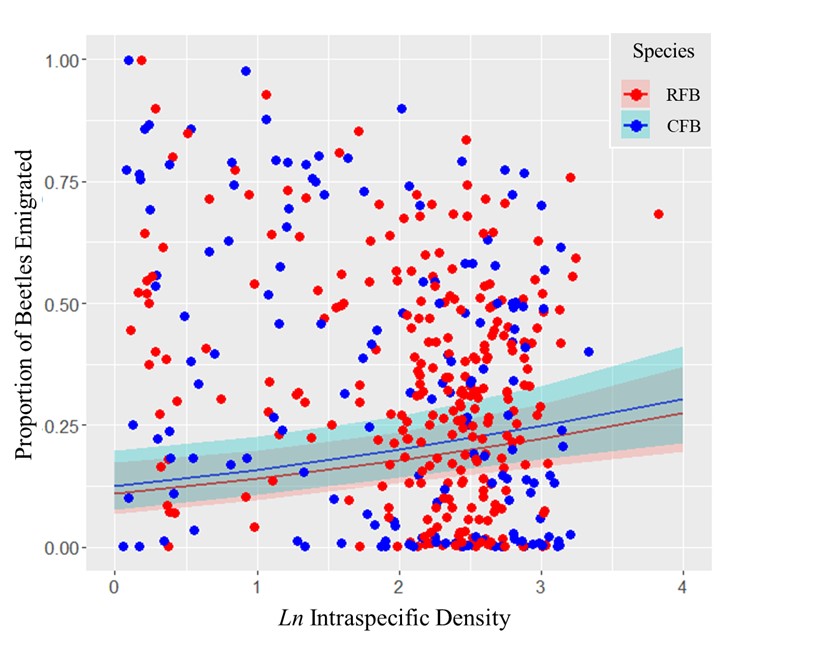
In the presence of the other species, RFB exhibited density-independent emigration with respect to either species density. The effects of conspecific and interspecific density on CFB were more complicated. CFB exhibited a -DDE response to RFB. But, CFB’s response to its own density changed in the presence of RFB - CFB density effects varied from hDDE to uDDE across the RFB density gradient (there was a strong RFB × CFB density interaction term on CFB emigration).
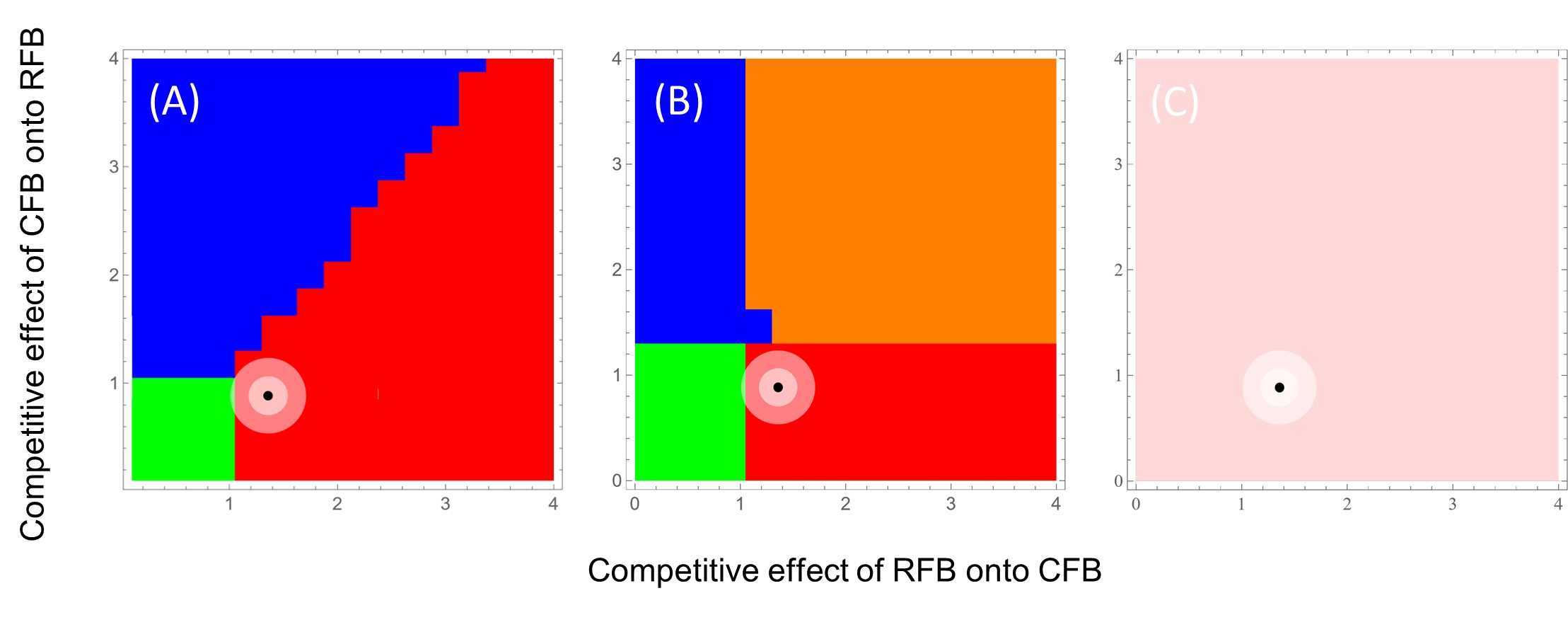
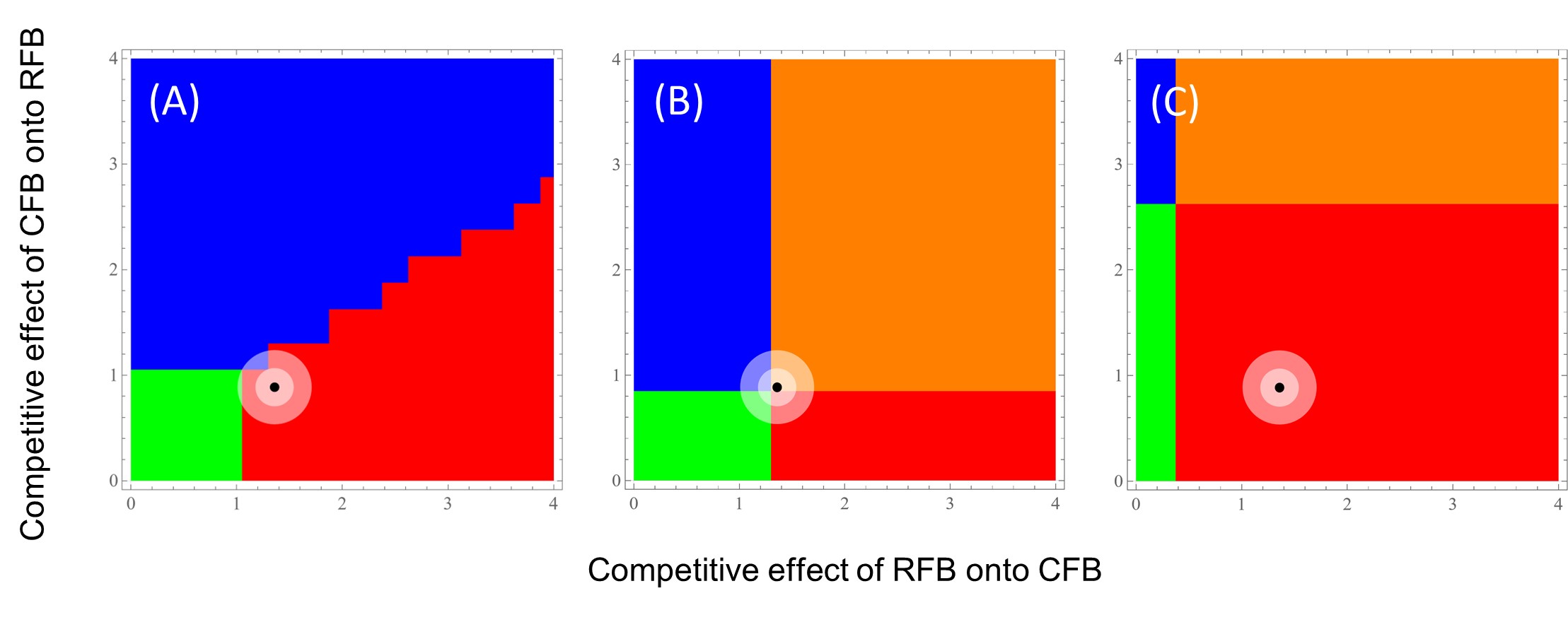
What do these varied density-dependent emigration effects have on the coexistence of RFB and CFB in the context of different patch sizes and patch permeabilities? We explored this question using a Lotka-Volterra reaction-diffusion model to determine the probabilistic long-term steady state dynamics for this two-species system. The model was parameterized with independent data from our Tribolium research and accounted for stochasticity in model parameters. In small patches, regardless of permeability level, RFB has nearly a 100% probability of being the winner in this competitive interaction (Fig. 5). However, in large patches, the outcome is not so certain, especially in the case where permeability is limited (i.e., the Low treatment). In this case, the mean expected outcome rests at the intersection between RFB winning, CFB winning, coexistence, and a priority effect whereby the first to arrive is the victor (Fig. 6). This study highlights the importance of context-dependent dispersal and stochastic effects on the competitive outcome for a species. A manuscript on this research is in preparation, with Aaron Krivchenia as the lead author.
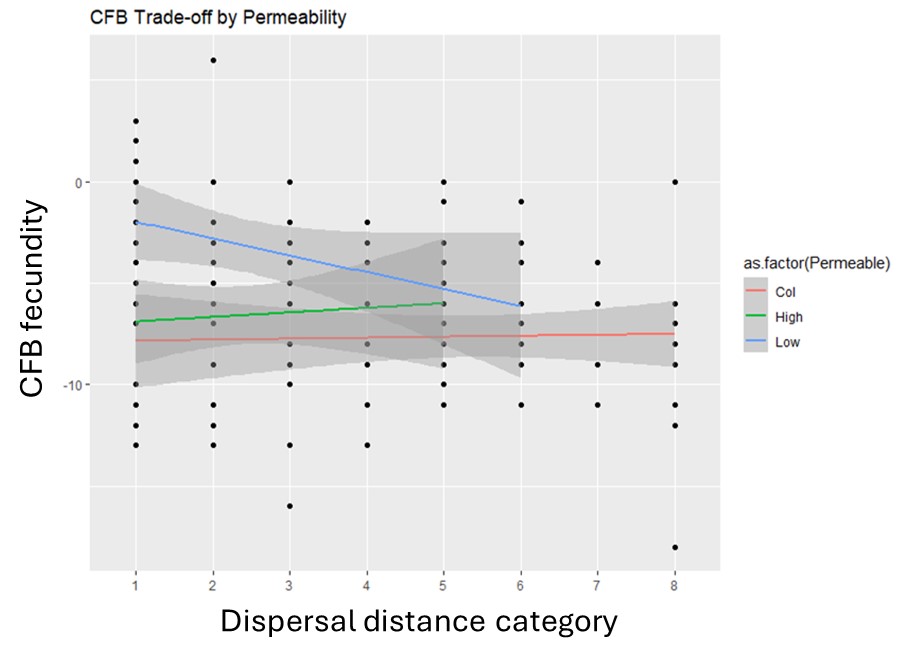
6. Life-history tradeoffs are likely involved in the coexistence of RFB and CFB in single-patch, open systems (Krivchenia et al. in preparation B). This study is based on the long-term experiment that was described previously in which Tribolium species composition (alone or together), patch size and patch permeability were manipulated. The emigration rate was monitored for each replicate and all treatment combinations and at generations 6, 12 and 18, Aaron assayed beetles to determine their body size, fecundity, emigration rate and competitive ability. The latter was determined by placing a single female of one species in the presence of 10 females of the other species and determining how many offspring she produced in the presence, relative to the absence, of the other species.
Aaron Krivchenia is the lead on this research and the final set of assays has only recently been completed. So, only the highlights can be reported at this time. As has been reported in the past, RFB was a significantly better competitor than CFB – well before generation 18, RFB displaced CFB in most mixed-species replicates. In addition, while we found no evidence of trade-offs for RFB, CFB did exhibit a trade-off in low permeability trials where fecundity decreased as distance traveled increased (Fig. 7).
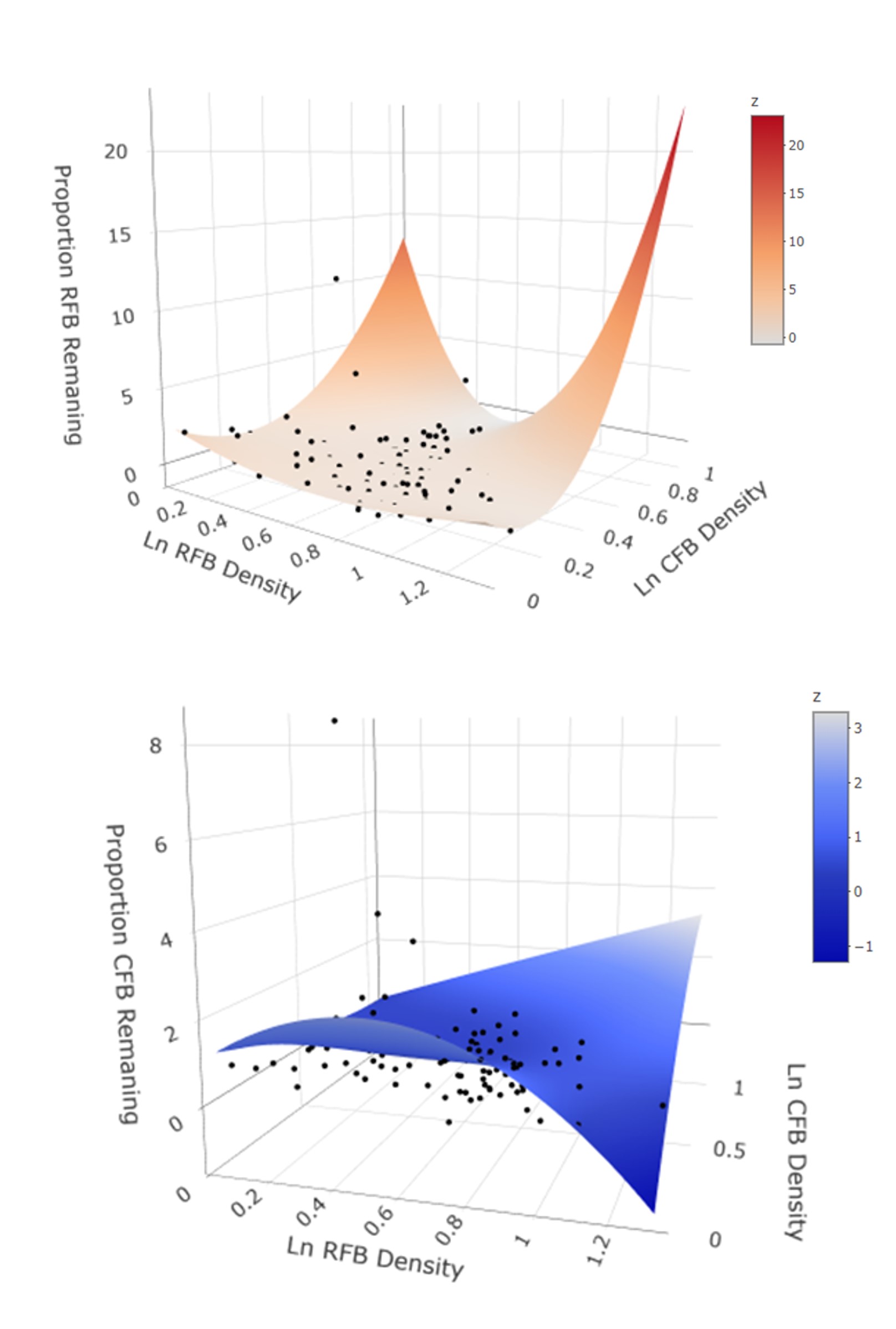
7. Conditional dispersal and coexistence of ci flour beetles in a multi-patch system (Krivchenia et al. in preparation C). We have extended the single-patch emigration study system with T. confusum and T. castaneum (alone and together) to a three-patch system (Fig. 8a). The system can also be modified to increase matrix hostility by creating dead ends in the dispersal tubes (Fig. 8b).

Over the course of 10 discrete generations, we found the following results. First, both species exhibited positive density-dependent emigration when released alone in the landscape. Second, when released together, both species’ dispersal response was nonlinear (Fig. 9). CFB had a small effect on RFB dispersal. However, RFB density and its interaction with CFB density had a large effect on CFB emigration. For CFB, CFB density and the interaction between CFB and RFB density had a strong effect on its emigration.
Competition and natural-enemy effects on emigration and population dynamics
8. Our models suggest that predator-induced prey dispersal can cause hump-shaped density-area relationships in prey populations (Cronin et al. 2024, J. Math Biol). Predation can both reduce prey abundance directly (through density-dependent effects) and indirectly through prey trait-mediated effects. We employed a theoretical spatially explicit predator– prey population model built upon the reaction-diffusion framework to explore effects of predator-induced emigration (trait-mediated emigration) and matrix hostility on DAR, minimum patch size, and species coexistence. Our results show that when trait-mediated response strength is sufficiently strong, ranges of patch size emerge where a nonlinear hump-shaped prey DAR is predicted and other ranges where coexistence is not possible. In a conservation perspective, DAR is crucial not only in deciding whether we should have one large habitat patch or several-small (SLOSS), but for understanding the minimum patch size that can support a viable population. Our study lends more credence to the possibility that predators can alter prey DAR through predator-induced prey dispersal.
9. Fungal entomopathogen density effects on the biology and movement behavior of two congeneric Tribolium species (Krivchenia et al. in preparation D). Aaron Krivchenia conducted a series of experiments investigating the density effects of a fungal pathogen, Beauveria bassiana, on the infectivity, survival and movement behavior of Tribolium castaneum and T. confusum. In the laboratory, the fungus had stronger pathogenic and lethal effects on T. confusum, the inferior competitor of T. castaneum. However, the rate of infection was similar between the two beetle species. Our results also indicate that an increase in exposure to higher fungal densities leads to a decrease in dispersal (measured as mean displacement) for T. confusum but not T. castaneum (Fig. 10). These results highlight the potential for pathogens to mediate species interactions through differential impacts on movement behavior, which may have important implications for population dynamics and competition outcomes in fragmented landscape. Aaron is currently working on a draft of this manuscript.






